Charakterystyka kapilarności i przykład w wodzie

The kapilarność Jest to właściwość cieczy, która pozwala im poruszać się przez otwory rurowe lub porowate powierzchnie nawet pod wpływem siły grawitacji. W tym celu musi istnieć równowaga i koordynacja dwóch sił związanych z cząsteczkami cieczy: spójność i adhezja; posiadanie tych dwóch fizycznych refleksji zwanych napięciem powierzchniowym.

Ciecz musi być w stanie zwilżyć wewnętrzne ścianki rury lub pory materiału, przez który się porusza. Dzieje się tak, gdy siła adhezji (ścianka cieczy w kapilarze) jest większa niż siła spójności międzycząsteczkowej. W konsekwencji cząsteczki cieczy tworzą silniejsze oddziaływania z atomami materiału (szkło, papier itp.) Niż między nimi.

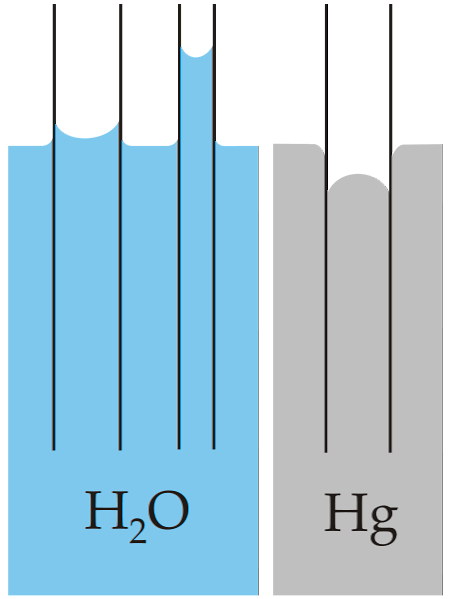
Klasyczny przykład kapilarności ilustruje porównanie tej właściwości dla dwóch bardzo różnych cieczy: wody i rtęci.

Górny obraz pokazuje, że woda podnosi się przez ściany rury, co oznacza, że ​​ma wyższe siły adhezji; natomiast w przypadku rtęci dzieje się odwrotnie, ponieważ jej spójne, metaliczne siły wiążące zapobiegają zwilżaniu szkła.

Z tego powodu woda tworzy wklęsły łąkotek, a rtęć wypukły łąkotek (w kształcie kopuły). Należy również zauważyć, że im mniejszy promień rury lub odcinka, przez który porusza się ciecz, tym większa wysokość lub przebyta odległość (porównaj wysokości słupów wody dla obu rur).

Indeks

• 1 Charakterystyka naczyń włosowatych
  • 1.1 - Powierzchnia cieczy
  • 1,2-Wysokość
  • 1.3 - Napięcie powierzchniowe
  • 1.4 -Radio kapilary lub porów, w której unosi się ciecz
  • 1.5 - Kąt zwilżania (θ)
• 2 Kapilarność wody
  • 2.1 Na roślinach
• 3 referencje

Charakterystyka naczyń włosowatych

-Powierzchnia cieczy

Powierzchnia cieczy, powiedzmy woda, w kapilarze jest wklęsła; to znaczy menisk jest wklęsły. Sytuacja taka ma miejsce, ponieważ wypadkowa sił wywieranych na cząsteczki wody w pobliżu ściany rury jest skierowana w tym kierunku.

We wszystkich meniskach występuje kąt zwilżania (θ), który jest kątem, który tworzy ścianę rurki kapilarnej z linią styczną do powierzchni cieczy w punkcie styku.

Siły adhezji i spójności

Jeśli siła adhezji cieczy do ściany kapilarnej przeważa nad siłą spójności międzycząsteczkowej, to kąt wynosi θ < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.

Gdy kropla wody zostanie umieszczona na powierzchni czystego szkła, woda rozprzestrzenia się na szybie, tak że θ = 0 i cos θ = 1.

Jeśli siła kohezji międzycząsteczkowej przeważa nad siłą przylegania kapilary do ściany cieczy, na przykład w rtęci, menisk będzie wypukły, a kąt θ będzie miał wartość> 90º; rtęć nie zwilża ściany kapilarnej i dlatego schodzi przez jej wewnętrzną ścianę.

Gdy kropla rtęci zostanie umieszczona na powierzchni czystego szkła, kropla zachowuje swój kształt i kąt θ = 140º.

-Wysokość

Woda podnosi się przez rurkę kapilarną, aby osiągnąć wysokość (h), w której masa słupa wody kompensuje pionową składową międzycząsteczkowej siły spójności.

W miarę wzrostu ilości wody nastąpi punkt, w którym grawitacja zatrzyma swój wzrost, nawet jeśli napięcie powierzchniowe działa na twoją korzyść.

Gdy tak się stanie, molekuły nie mogą dalej „wspinać się” po wewnętrznych ścianach, a wszystkie siły fizyczne zostają wyrównane. Z jednej strony masz siły, które sprzyjają wzrostowi wody, az drugiej strony twój własny ciężar popycha go w dół.

Prawo Jurina

Można to zapisać matematycznie w następujący sposób:

2 π rΥcosθ = ρgπr²h

Gdzie lewa strona równania zależy od napięcia powierzchniowego, którego wielkość jest również powiązana z kohezją lub siłami międzycząsteczkowymi; Cosθ oznacza kąt zwilżania, a r promień otworu, przez który płynie ciecz.

A po prawej stronie równania mamy wysokość h, siłę grawitacji g i gęstość cieczy; to byłaby woda.

Czyszczenie to h masz

h = (2Υcosθ / ρgr)

Ta formuła jest znana jako prawo Jurina, które określa wysokość osiągniętą przez kolumnę cieczy w rurce kapilarnej, gdy waga kolumny cieczy jest równoważona siłą wznoszenia przez kapilarność.

-Napięcie powierzchniowe

Woda jest cząsteczką dipolarną ze względu na elektroujemność atomu tlenu i jego geometrię molekularną. Powoduje to, że część cząsteczki wody, w której znajduje się tlen, jest naładowana ujemnie, podczas gdy część cząsteczki wody, zawierająca 2 atomy wodoru, jest naładowana dodatnio.

Cząsteczki w cieczy oddziałują dzięki temu poprzez wiele wiązań wodorowych, utrzymując je razem. Jednak cząsteczki wody znajdujące się w wodzie międzyfazowej: powietrze (powierzchnia) są poddawane przyciąganiu netto przez cząsteczki płynnej zatoki, nie kompensowane słabym przyciąganiem cząsteczek powietrza..

Zatem cząsteczki wody interfejsu są poddawane sile przyciągania, która ma tendencję do usuwania cząsteczek wody z interfejsu; to znaczy mostki wodorowe utworzone z molekułami na dole ciągną te, które są na powierzchni. Zatem napięcie powierzchniowe dąży do zmniejszenia powierzchni interfejsu woda: powietrze.

Związek z h

Jeśli spojrzysz na równanie prawa Jurina, przekonasz się, że h jest wprost proporcjonalne do Υ; dlatego im większe napięcie powierzchniowe cieczy, tym większa wysokość, która może wzrosnąć przez kapilarę lub por materiału.

Można zatem oczekiwać, że dla dwóch cieczy, A i B, o różnych napięciach powierzchniowych, ta o najwyższym napięciu powierzchniowym wzrośnie do wyższej wysokości.

Z tego punktu można wywnioskować, że wysokie napięcie powierzchniowe jest najważniejszą cechą, która określa właściwość kapilarną cieczy.

-Promień kapilary lub porów, w których unosi się ciecz

Obserwacja Prawa Jurina wskazuje, że wysokość osiągnięta przez ciecz w kapilarze lub porach jest odwrotnie proporcjonalna do promienia tego samego.

Dlatego im mniejszy promień, tym większa wysokość, na jaką kolumna cieczy osiągnie działanie kapilarne. Można to zobaczyć bezpośrednio na obrazie, w którym woda jest porównywana z rtęcią.

W szklanej rurce o promieniu 0,05 mm słup wody pod wpływem kapilarności osiągnie wysokość 30 cm. W rurkach kapilarnych o promieniu 1 μm przy ciśnieniu ssania 1,5 x 10³ hPa (która jest równa 1,5 atm) odpowiada obliczeniu wysokości słupa wody od 14 do 15 m.

Jest to bardzo podobne do tego, co dzieje się z tymi słomkami, które obracają się same w sobie kilka razy. Przez zasysanie cieczy powstaje różnica ciśnień, która powoduje, że ciecz podnosi się do ust.

Maksymalna wartość wysokości kolumny osiągniętej przez kapilarność jest teoretyczna, ponieważ promień naczyń włosowatych nie może być zmniejszony poza pewną granicę.

Prawo Poiseuille

Stwierdza to, że przepływ prawdziwej cieczy wynika z następującego wyrażenia:

Q = (πr⁴/ 8ηl) PP

Gdzie Q jest przepływem cieczy, η to jego lepkość, l długość rury, a ΔP różnica ciśnień.

Przy zmniejszaniu promienia kapilary wysokość kolumny cieczy osiągnięta przez kapilarność powinna wzrastać w nieskończoność. Jednak Poiseuille wskazuje, że zmniejszenie promienia zmniejsza również przepływ cieczy przez tę kapilarę.

Ponadto lepkość, która jest miarą oporu, który przeciwstawia się przepływowi prawdziwej cieczy, dodatkowo zmniejszyłaby przepływ cieczy.

-Kąt kontaktu (θ)

Im wyższa wartość cosθ, tym wyższa wysokość słupa wody przez kapilarność, jak wskazuje prawo Jurina.

Jeśli θ jest małe i zbliża się do zera (0), cosθ wynosi = 1, więc wartość h będzie maksymalna. Przeciwnie, jeśli if jest równe 90º, cosθ = 0, a wartość h = 0.

Gdy wartość θ jest większa niż 90º, co ma miejsce w przypadku wypukłej menisku, ciecz nie unosi się przez kapilarność i jej tendencja do opadania (jak ma to miejsce w przypadku rtęci).

Kapilarność wody

Woda ma wartość napięcia powierzchniowego 72,75 N / m, stosunkowo wysoką w porównaniu z wartościami napięcia powierzchniowego następujących cieczy:

-Aceton: 22,75 N / m

-Alkohol etylowy: 22,75 N / m

-Heksan: 18,43 N / m

-Metanol: 22,61 N / m.

Dlatego woda ma wyjątkowe napięcie powierzchniowe, co sprzyja rozwojowi zjawiska kapilarnego tak niezbędnego do absorpcji wody i składników odżywczych przez rośliny.

Na rośliny

Naczynie włoskowate jest ważnym mechanizmem wzrostu soku przez ksylem roślin, ale samo w sobie nie wystarcza, aby sok sięgnął liści drzew.

Transpiracja lub parowanie jest ważnym mechanizmem w wynurzaniu soku przez ksylem roślin. Liście tracą wodę przez odparowanie, powodując spadek ilości cząsteczek wody, co powoduje przyciąganie cząsteczek wody obecnych w rurkach kapilarnych (ksylem).

Cząsteczki wody nie działają niezależnie od siebie, ale oddziałują siłami Van der Waalsa, co powoduje, że wznoszą się one połączone rurkami kapilarnymi roślin w kierunku liści.

Oprócz tych mechanizmów należy zauważyć, że rośliny pochłaniają wodę z gleby przez osmozę i że dodatnie ciśnienie wytwarzane w korzeniu napędza początek wynurzania wody przez naczynia włosowate rośliny.

Referencje

1. García Franco A. (2010). Zjawiska powierzchowne. Źródło: sc.ehu.es
2. Zjawiska powierzchniowe: napięcie powierzchniowe i kapilarność. [PDF] Źródło: ugr.es
3. Wikipedia. (2018). Kapilarność Źródło: en.wikipedia.org
4. Risvhan T. (s.f.) Kapilarność roślin. Źródło: academia.edu
5. Helmenstine, Anne Marie, Ph.D. (22 grudnia 2018 r.). Działanie kapilarne: definicja i przykłady. Źródło: thinkco.com
6. Ellen Ellis M. (2018). Działanie naczyń włosowatych: definicja i przykłady. Studiować Źródło: study.com
7. Personel ScienceStruck. (16 lipca 2017). Przykłady, które wyjaśniają koncepcję i znaczenie działania naczyń włosowatych. Źródło: sciencestruck.com