Archimedes Biography, Contributions and Inventions
Archimedes z Syrakuz (287 a.C - 212 a.C) był matematykiem, fizykiem, wynalazcą, inżynierem i greckim astronomem ze starożytnego miasta Syrakuzy na Sycylii. Jego najwybitniejszym wkładem jest zasada Archimedesa, rozwój metody ostrzegania, metoda mechaniczna lub stworzenie pierwszego planetarium.
W tej chwili jest uważany za jedną z trzech ważniejszych postaci matematyki starożytności obok Euklidesa i Apolonio, ponieważ jego wkład oznaczał ważne osiągnięcia naukowe w dziedzinie obliczeń, fizyki, geometrii i astronomii. To z kolei czyni go jednym z najwybitniejszych naukowców w historii ludzkości.

Chociaż znane są nieliczne szczegóły jego życia osobistego - a te, które są znane, mają wątpliwą wiarygodność - jego wkład jest znany dzięki serii pisemnych listów o jego dziełach i osiągnięciach, które zostały zachowane do czasów obecnych, należących do do korespondencji, którą prowadził przez lata z przyjaciółmi i innymi matematykami tamtych czasów.
Archimedes był znany w swoim czasie dzięki swoim wynalazkom, które przyciągnęły uwagę współczesnych, częściowo dlatego, że były używane jako urządzenia wojenne, aby skutecznie uniknąć licznych najazdów rzymskich..
Mówi się jednak, że twierdził, że jedyną naprawdę ważną rzeczą jest matematyka i że jego wynalazki są jedynie produktem rozrywki stosowanej geometrii. W potomności jego dzieła w czystej matematyce były znacznie bardziej doceniane niż jego wynalazki.
Indeks
- 1 Biografia
- 1.1 Szkolenie
- 1.2 Prace naukowe
- 1.3 Konflikt w Syrakuzach
- 1.4 Śmierć
- 2 Wkład naukowy Archimedesa
- 2.1 Zasada Archimedesa
- 2.2 Metoda mechaniczna
- 2.3 Wyjaśnienie prawa dźwigni
- 2.4 Opracowanie metody ostrzegania lub wyczerpywania demonstracji naukowej
- 2.5 Miara okręgu
- 2.6 Geometria kulek i cylindrów
- 3 wynalazki
- 3.1 Licznik kilometrów
- 3.2 Pierwsze planetarium
- 3.3 Śruba Archimedesa
- 3.4 Szpon Archimedesa
- 4 odniesienia
Biografia
Archimedes z Syracuse urodził się mniej więcej w roku 287 pne. Niewiele wiadomo o jego wczesnych latach, choć można powiedzieć, że urodził się w Syrakuzach, mieście uważanym za główny port morski Sycylii, dziś we Włoszech..
W tym czasie Syrakuzy były jednym z miast, które tworzyły tzw. Magna Grecia, przestrzeń zamieszkałą przez osadników pochodzenia greckiego w południowej części półwyspu Włoch i Sycylii.
Nie ma znanych faktów dotyczących matki Archimedesa. W odniesieniu do ojca wiadomo, że nazywano go Phidias i że poświęcił się astronomii. Ta informacja o jego ojcu jest znana dzięki fragmentowi książki Licznik piasku, napisany przez Archimedesa, w którym wspomina imię ojca.
Heraklides, grecki filozof i astronom, bardzo lubił Archimedesa, a nawet napisał o nim biografię. Dokument ten nie został jednak zachowany, więc wszystkie zawarte w nim informacje są nieznane.
Z drugiej strony, historyk, filozof i biograf Plutarco wskazał w swojej książce Parallel Lives, że Archimedes miał związek krwi z Hiero II, tyranem, który rządził w Syrakuzach od 265 pne.
Szkolenie
Dzięki małym informacjom o Archimedesie nie wiemy na pewno, gdzie uzyskał pierwsze szkolenie.
Jednak różni historiografowie ustalili, że istnieje duże prawdopodobieństwo, że Archimedes studiował w Aleksandrii, która była najważniejszym greckim centrum kulturalnym i pedagogicznym w regionie..
To założenie jest poparte informacją greckiego historyka Diodoro Sículo, który wskazał, że Archimedes prawdopodobnie studiował w Aleksandrii.
Ponadto w wielu swoich pracach sam Archimedes wspomina o innych naukowcach tamtych czasów, których prace koncentrowały się w Aleksandrii, więc można założyć, że rzeczywiście rozwinął się w tym mieście.
Niektóre z osobowości, z którymi Archimedes miał kontakt w Aleksandrii, to geograf, matematyk i astronom Eratostenes z Cyreny oraz matematyk i astronom Conon de Sanos.
Motywacja rodzinna
Z drugiej strony fakt, że ojciec Archimedesa był astronomem, mógł mieć znaczący wpływ na skłonności, które później wykazał, ponieważ później i od najmłodszych lat istniała szczególna atrakcja w dziedzinie nauki ścisłe.
Szacuje się, że po swoim czasie w Aleksandrii Archimedes powrócił do Syrakuz.
Praca naukowa
Po powrocie do Syracuse Archimedes zaczął opracowywać różne artefakty, które wkrótce zyskały mu pewną popularność wśród mieszkańców tego miasta. W tym okresie oddał się całkowicie pracy naukowej, wyprodukował różne wynalazki i wydedukował kilka pojęć matematycznych bardzo zaawansowanych w swoim czasie.
Na przykład, kiedy poświęcił się badaniu cech bryłowych i płaskich figur, wymyślił koncepcje związane z rachunkiem całkowym i różniczkowym, które opracowano później.
Również Archimedes był tym, który zdefiniował, że objętość związana z kulą odpowiada dwukrotności rozmiaru zawierającego ją cylindra, i to on wynalazł kompozytowe koło pasowe, w oparciu o jego odkrycia dotyczące prawa dźwigni.
Konflikt w Syracuse
W roku 213 pne rzymscy żołnierze wkroczyli do miasta Syrakuzy i otoczyli osadników, aby ich poddać.
Ta akcja była prowadzona przez wojskowego i greckiego polityka Marco Claudio Marcelo w ramach drugiej wojny punickiej. Później był znany jako Miecz Rzymu, ponieważ zakończył się zdobyciem Syrakuz.
W środku konfliktu, który trwał dwa lata, mieszkańcy Syrakuz walczyli z Rzymianami z odwagą i zaciekłością, a Archimedes odegrał bardzo ważną rolę, biorąc pod uwagę, że poświęcił się tworzeniu narzędzi i instrumentów, które pomogły pokonać Rzymian.
Wreszcie Marco Claudio Marcelo przejął miasto Syracuse. Przed wielką intelektualnością Archimedesa Marcelo rozkazał, by nie zostali ranni ani zabici. Jednak Archimedes został zabity w rękach rzymskiego żołnierza.
Śmierć
Archimedes zmarł w roku 212 pne. Ponad 130 lat po jego śmierci, w roku 137 pne pisarz, polityk i filozof Marco Tulio Cicero zajmował stanowisko w administracji Rzymu i chciał znaleźć grobowiec Archimedesa.
To zadanie nie było łatwe, ponieważ Cicero nie mógł znaleźć nikogo, kto wskazałby dokładne miejsce. Ostatecznie jednak udało mu się go zdobyć, bardzo blisko drzwi Agrigento i w opłakanych warunkach.
Cicero oczyścił grobowiec i odkrył, że został on wpisany w kulę wewnątrz cylindra, jako odniesienie do odkrycia o objętości, którą Archimedes zrobił jakiś czas temu..
Wersje dotyczące jego śmierci
Pierwsza wersja
Jedna z wersji mówi, że Archimedes był w trakcie rozwiązywania problemu matematycznego, kiedy podszedł do niego rzymski żołnierz. Mówi się, że Archimedes mógł go poprosić o rozwiązanie problemu, więc żołnierz go zabił.
Druga wersja
Druga wersja jest podobna do pierwszej. Rachunek, że Archimedes rozwiązywał problem matematyki, gdy miało miejsce zajęcie miasta.
Rzymski żołnierz wszedł do jego kompleksu i kazał mu spotkać się z Marcelo, a Archimedes odpowiedział, że najpierw musi rozwiązać problem, nad którym pracował. Żołnierz zdenerwował się w wyniku tej reakcji i zabił go.
Trzecia wersja
Hipoteza ta wskazuje, że Archimedes miał w swoich rękach wielką różnorodność instrumentów typowych dla matematyki. Potem zobaczył go żołnierz i pomyślał, że może nosić cenne przedmioty, więc go zabił.
Czwarta wersja
Ta wersja pokazuje, że Archimedes przykucnął przy ziemi, rozważając plany, które studiował. Najwyraźniej rzymski żołnierz przybył z tyłu i nieświadomy, że to Archimedes, zastrzelił go.
Wkład naukowy Archimedesa
Zasada Archimedesa
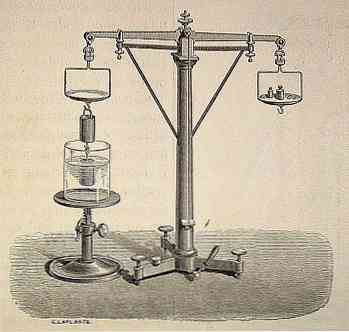
Współczesna nauka uznaje Archimedesa za jedną z najważniejszych spuścizn starożytnej epoki.
W całej historii i ustnie donoszono, że Archimedes przypadkowo doszedł do swego odkrycia dzięki królowi Hieronowi, który zlecił sprawdzenie, czy złota korona, wysłana przez niego do produkcji, została tylko złota czysty i nie zawierał żadnego innego metalu. Musiałem to zrobić bez niszczenia korony.
Mówi się, że podczas gdy Archimedes medytował, jak rozwiązać ten problem, postanowił się wykąpać, a kiedy wszedł do wanny, uświadomił sobie, że poziom wody wzrósł, gdy się w niej zanurzył..
W ten sposób odkryłby naukową zasadę, że „każde ciało zanurzone całkowicie lub częściowo w płynie (płynie lub gazie) otrzymuje napór w górę, równy ciężarowi płynu usuniętego przez przedmiot”.
Zasada ta oznacza, że płyny wywierają siłę wstępującą - pchając w górę - na każdy zanurzony w nich przedmiot, a ilość tej siły pchającej jest równa masie cieczy wypartej przez zanurzone ciało, niezależnie od jego masy.
Wyjaśnienie tej zasady opisuje zjawisko flotacji i znajduje się w jego Traktat o ciałach pływających.
Zasada Archimedesa została w znacznym stopniu zastosowana w potomności do unoszenia się obiektów masowego użytku, takich jak okręty podwodne, statki, ratownicy i balony.
Metoda mechaniczna
Kolejnym z najważniejszych wkładów do nauki Archimedesa było włączenie metody czysto mechanicznym -to znaczy, rozumowania i argumentacji technicznej problemów geometrycznych, co oznaczało, bezprecedensowy sposób, aby rozwiązać te problemy w czasie.
W kontekście Archimedesa geometria była uważana za naukę wyłącznie teoretyczną, a powszechną rzeczą było to, że czysta matematyka była zstąpiona w kierunku innych nauk praktycznych, w których można zastosować jej zasady..
Z tego powodu dziś jest uważany za prekursora mechaniki jako dyscypliny naukowej.
Na piśmie, w którym matematyk ujawnia nową metodę swojemu przyjacielowi Eratostenesowi, wskazuje, że pozwala to zająć się zagadnieniami matematyki poprzez mechanikę i że nieco łatwiej jest zbudować demonstrację twierdzenia geometrycznego, jeśli już jest mieć wcześniejszą wiedzę praktyczną, że jeśli nie masz o tym pojęcia.
Ta nowa metoda badania przeprowadzona przez Archimedesa stałaby się prekursorem nieformalnego etapu odkrywania i formułowania hipotez nowoczesnej metody naukowej.
Wyjaśnienie prawa dźwigni
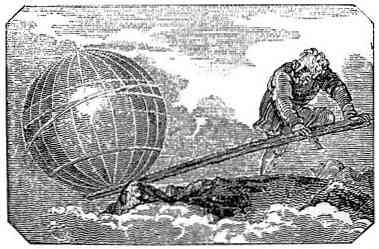
Podczas gdy dźwignia jest prostą maszyną, która była używana znacznie wcześniej niż Archimedes, to on sformułował zasadę, która wyjaśnia jej działanie w traktacie O równowadze samolotów.
W formułowaniu tego prawa Archimedes ustanawia zasady, które opisują różne zachowanie dźwigni podczas umieszczania na niej dwóch ciał, w zależności od wagi i odległości od punktu podparcia.
W ten sposób wskazuje, że dwa ciała, które można zmierzyć (współmierne), umieszczone na dźwigni, są zrównoważone, gdy znajdują się w odległości odwrotnie proporcjonalnej do ich wagi.
W ten sam sposób, niezmierzone ciała (których nie można zmierzyć) czynią to, ale prawo to zostało udowodnione przez Archimedesa tylko ciałami pierwszego typu.
Sformułowanie zasady dźwigni jest dobrym przykładem zastosowania metody mechanicznej, ponieważ zgodnie z tym, co wyjaśnia w liście skierowanym do Dositeo, ten został odkryty w pierwszej chwili za pomocą metod mechaniki, które wprowadziły w życie.
Później sformułował je metodami geometrii (teoretycznej). Z tego eksperymentu na ciałach oddzielono również pojęcie środka ciężkości.
Opracowanie metody ostrzegania lub wyczerpania demonstracji naukowej
Wyczerpanie jest metodą stosowaną w geometrii, która polega na aproksymacji figur geometrycznych, których powierzchnia jest znana za pomocą napisu i okręgu na innym, którego obszar ma być znany..
Chociaż Archimedes nie był twórcą tej metody, opracował ją po mistrzowsku, potrafiąc obliczyć za jej pomocą dokładną wartość Pi.
Archimedes, stosując metodę ostrzeżenia, wpisane i opisane sześciokąty na obwodzie o średnicy 1, zmniejszając do absurdu różnicę między obszarem sześciokątów a obszarem obwodu.
Aby to zrobić, przeciął sześciokąty, tworząc wielokąty o maksymalnie 16 bokach, jak pokazano na poprzednim rysunku.
W ten sposób doszedł do określenia, że wartość pi (relacji między długością okręgu a jego średnicą) mieści się między wartościami 3.14084507 ... i 3.14285714 ... .
Archimedes mistrzowsku wykorzystał metodę wyczerpania, ponieważ nie tylko udało podejście do obliczania wartości Pi z marginesem błędu bardzo niski i dlatego deseado- ale również za to, że liczbą niewymierną przez Pi ta metoda oraz uzyskane wyniki podwaliny do kiełkowania w rachunku systemu, a następnie, w nowoczesnej całkowego.
Miara okręgu
Aby określić obszar okręgu, Archimedes użył metody polegającej na narysowaniu kwadratu, który dokładnie pasuje do okręgu.
Wiedząc, że powierzchnia kwadratu była sumą jego boków i że obszar okręgu był większy, zaczął pracować nad uzyskaniem przybliżeń. Zrobił to, zastępując kwadrat sześciobocznym wielokątem, a następnie pracując z bardziej złożonymi wielokątami.
Archimedes był pierwszym matematykiem w historii, który podszedł do poważnego obliczenia liczby Pi.
Geometria kulek i cylindrów
Wśród dziewięciu traktatów kompilujących pracę Archimedesa w matematyce i fizyce są dwa tomy dotyczące geometrii kulek i cylindrów.
Praca ta dotyczy określenia, że powierzchnia dowolnej kuli o promieniu jest czterokrotnie większa od jej największego koła, a objętość kuli wynosi dwie trzecie średnicy cylindra, w którym jest wpisana.
Wynalazki
Licznik kilometrów
Znany również jako kilometry, był wynalazkiem tego słynnego człowieka.
To urządzenie zbudowano w oparciu o zasadę koła, które po obróceniu aktywuje koła zębate, które pozwalają obliczyć przebytą odległość..
Zgodnie z tą samą zasadą Archimedes zaprojektował kilka rodzajów liczników kilometrów do celów wojskowych i cywilnych.
Pierwsze planetarium
Na podstawie zeznań wielu klasycznych pisarzy jak Cicero, Owidiusza Claudian Marciano Capela Casiodoro, Sekstus Empiryk i Lactancio, dziś wielu naukowców przypisują Archimedesa utworzenie pierwszego szczątkowej planetarnej.
Jest to mechanizm składający się z szeregu „sfer”, które potrafiły naśladować ruch planet. Do tej pory szczegóły tego mechanizmu są nieznane.
Według Cycerona planetaria zbudowane przez Archimedesa były dwa. W jednym z nich reprezentowano ziemię i różne konstelacje w jej pobliżu.
W drugim, przy jednym obrocie, słońce, księżyc i planety wykonały swoje własne niezależne ruchy w stosunku do gwiazd stałych w taki sam sposób, jak w prawdziwym dniu. W tym drugim można ponadto zaobserwować kolejne fazy i zaćmienia księżyca.
Śruba Archimedesa
Śruba Archimedesa jest urządzeniem służącym do transportu wody od dołu do góry przez zbocze, za pomocą rury lub cylindra.
Według greckiego historyka Diodoro, dzięki temu wynalazkowi ułatwiono nawadnianie żyznych ziem położonych wzdłuż rzeki Nil w starożytnym Egipcie, ponieważ tradycyjne narzędzia wymagały ogromnego wysiłku fizycznego, który wyczerpał robotników.
Zastosowany cylinder ma śrubę o tej samej długości, która utrzymuje połączony system śmigieł lub żeber, które wykonują ruch obrotowy napędzany ręcznie przez obrotową dźwignię.
W ten sposób helisy potrafią wypchnąć dowolną substancję od dołu, tworząc rodzaj nieskończonego obwodu.
Szpon Archimedesa
Szpon Archimedesa lub żelazna ręka, jak jest również znana, był jedną z najbardziej przerażających broni wojennych stworzonych przez tego matematyka, stając się najważniejszą dla sycylijskiej obrony najazdów rzymskich.
Według badań przeprowadzonych przez profesorów z Uniwersytetu Drexel Chris Rorres (Wydział Matematyki) i Harry Harris (Wydział Inżynierii Lądowej i Architektury), to było wielkie dźwigni, który miał hak przymocowany do dźwigni przez łańcuch wokół niej.
Za pośrednictwem dźwigni tak, że hak spadł na statek wroga była manipulowana, a celem było podłączyć go i podnieść ją do tego stopnia, że zwolnienie zostało osiągnięte całkowicie przewrócić lub spowodować awarię na skałach brzegu.
Rorres i Harris zaprezentowane na sympozjum „Maszyny i niezwykłych budowli starożytności” (2001), miniaturowe reprezentacji tego urządzenia zatytułowany „potężną machinę wojenną: Budowa i eksploatacja żelazną ręką Archimedesa”
Dla realizacji tej pracy oparli się na argumentach starożytnych historyków Polibio, Plutarco i Tito Livio.
Referencje
- ASSIS, A. (2008). Archimedes, środek ciężkości i pierwsze prawo mechaniki [online]. Dostęp 10 czerwca 2017 r. Na bourabai.ru.
- DIJKSTERHUIS, E. (1956). Archimedes [online]. Dostęp 9 czerwca 2015 r. W sieci World Wide Web: books.google.co.ve/books.
- MOLINA, A. (2008). Metoda badawcza Archimedesa z Syrakuz: intuicja, mechanika i uwaga [online]. Dostęp 10 czerwca 2017 r. W World Wide Webproduccioncientifica.luz.edu.
- O'CONNOR, J. i ROBERTSON, R. (1999). Archimedes z Syracuse [online]. Dostęp 9 czerwca 2017 r. Na stronie history.mcs.st-and.ac.uk.
- PARRA, E. (2009). Archimedes: jego życie, prace i wkład w nowoczesną matematykę [online]. Pobrane 9 czerwca 2017 r. W lfunes.uniandes.edu.co.
- QUINN, L. (2005). Archimedes z Syracuse [online]. Dostęp 9 czerwca 2017 w math.ucdenver.edu.
- RORRES, C. i HARRIS, H. (2001). Ogromna machina wojenna: budowa i działanie żelaznej dłoni Archimedesa [online]. Źródło: 10 czerwca 2017 w cs.drexel.edu.
- VITE, L. (2014). Zasada Archimedesa [online]. Pobrane 10 czerwca 2017 r. W repository.uaeh.edu.mx.


