Układ współrzędnościowy i przykłady
The wektory kolinearne Są one jednym z trzech typów istniejących wektorów. Chodzi o te wektory, które są w tym samym kierunku lub linii działania. Oznacza to, że dwa lub więcej wektorów będzie współliniowych, jeśli są ułożone w linie proste, które są do siebie równoległe.
Wektor jest definiowany jako ilość zastosowana do ciała i charakteryzuje się tym, że ma kierunek, sens i skalę. Wektory można znaleźć w płaszczyźnie lub w przestrzeni i mogą być różnych typów: wektorów kolinearnych, wektorów współbieżnych i wektorów równoległych.

Indeks
- 1 wektor kolinealny
- 2 Charakterystyka
- 2.1 Przykład 1
- 2.2 Przykład 2
- 2.3 Przykład 1
- 3 Kolinearny system wektorowy
- 3.1 Wektory współliniowe z przeciwnymi zmysłami
- 3.2 Wektory kolinearne o tym samym znaczeniu
- 3.3 Wektory współliniowe o równych wielkościach i przeciwnych zmysłach
- 4 Różnica między wektorami współliniowymi i współbieżnymi
- 5 referencji
Wektory współliniowe
Wektory są współliniowe, jeśli linia działania jednego jest dokładnie tą samą linią działania wszystkich innych wektorów, niezależnie od wielkości i sensu każdego z wektorów.
Wektory są używane jako reprezentacje w różnych obszarach, takich jak matematyka, fizyka, algebra, a także w geometrii, gdzie wektory są kolinearne tylko wtedy, gdy ich kierunek jest taki sam, niezależnie od tego, czy ich znaczenie nie jest.
Funkcje
- Dwa lub więcej wektorów jest współliniowych, jeśli relacja między współrzędnymi jest równa.
Przykład 1
Mamy wektory m = m_x; m_y i n = n_x; n_y. Są one współliniowe, jeśli:
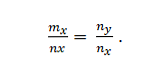
Przykład 2
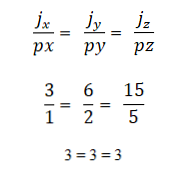
- Dwa lub więcej wektorów jest współliniowych, jeśli iloczyn produktu lub wektora jest równy zero (0). Dzieje się tak, ponieważ w układzie współrzędnych każdy wektor charakteryzuje się odpowiednimi współrzędnymi, a jeśli są one proporcjonalne do siebie, wektory będą współliniowe. Wyraża się to następująco:
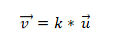
Przykład 1
Mamy wektory a = (10, 5) i b = (6, 3). Aby ustalić, czy są one współliniowe, stosuje się teorię determinant, która ustanawia równość produktów krzyżowych. W ten sposób musisz:
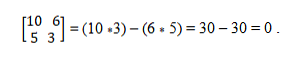
Kolinearny system wektorowy
Wektory współliniowe są reprezentowane graficznie przy użyciu kierunku i sensu tych wektorów, biorąc pod uwagę, że muszą przechodzić przez punkt aplikacji i moduł, który ma określoną skalę lub długość.
System wektorów współliniowych powstaje, gdy dwa lub więcej wektorów działa na obiekt lub ciało, reprezentując siłę i działając w tym samym kierunku.
Na przykład, jeśli dwie siły współliniowe są przykładane do ciała, wypadkowa tych sił będzie zależeć tylko od kierunku, w którym działają. Istnieją trzy przypadki:
Wektory współliniowe z przeciwnymi zmysłami
Wypadkowa dwóch wektorów współliniowych jest równa sumie tych:
R = Σ F = F1 + F2.
Przykład
Jeśli dwie siły działają na wózek F1 = 40 N i F2 = 20 N w przeciwnym kierunku (jak pokazano na zdjęciu), wynikiem jest:
R = Σ F = (- 40 N) + 20N.
R = - 20 N.
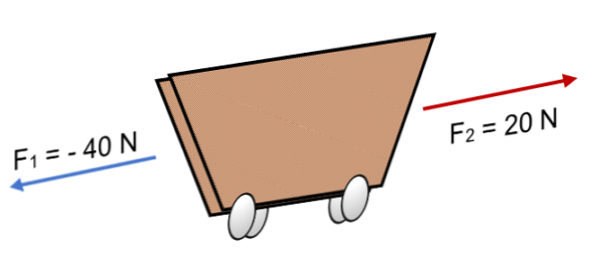
Wektory kolinearne o tym samym znaczeniu
Wielkość wypadkowej siły będzie równa sumie wektorów współliniowych:
R = Σ F = F1 + F2.
Przykład
Jeśli dwie siły działają na wózek F1 = 35 N i F2 = 55 N w tym samym kierunku (jak pokazano na zdjęciu), wynikiem jest:
R = Σ F = 35 N + 55N.
R = 90 N.
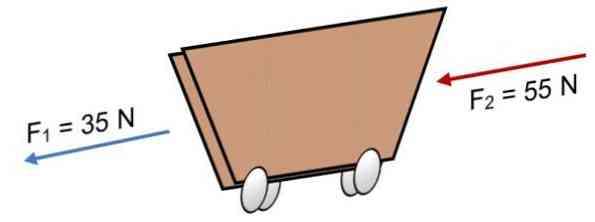
Wynik dodatni wskazuje, że wektory współliniowe działają w lewo.
Wektory współliniowe o równych wielkościach i przeciwnych zmysłach
Wypadkowa dwóch wektorów współliniowych będzie równa sumie wektorów współliniowych:
R = Σ F = F1 + F2.
Ponieważ siły mają tę samą wielkość, ale w przeciwnym kierunku - to znaczy, jeden będzie dodatni, a drugi ujemny - podczas dodawania dwóch sił wypadkowa będzie równa zero.
Przykład
Jeśli dwie siły działają na wózek F1 = -7 N i F2 = 7 N, które mają tę samą wielkość, ale w przeciwnym kierunku (jak pokazano na zdjęciu), wynikiem jest:
R = Σ F = (-7 N) + 7N.
R = 0.
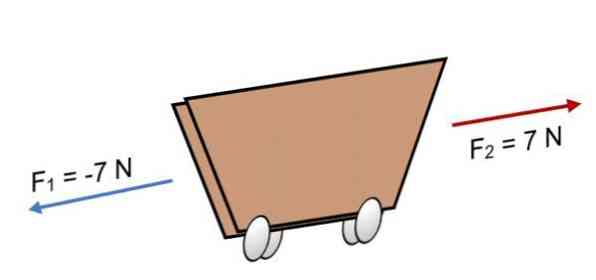
Ponieważ wypadkowa jest równa 0, oznacza to, że wektory są zrównoważone względem siebie, a zatem ciało jest w równowadze lub w spoczynku (nie poruszy się).
Różnica między wektorami współliniowymi i współbieżnymi
Wektory współliniowe charakteryzują się tym samym kierunkiem na tej samej linii lub są równoległe do linii; to znaczy, że są wektorami równoległymi.
Z drugiej strony, współbieżne wektory są definiowane, ponieważ znajdują się w różnych liniach działania, które są przechwytywane w jednym punkcie.
Innymi słowy, mają ten sam punkt początkowy lub przybycia - niezależnie od ich modułu, kierunku lub kierunku - tworząc między nimi kąt.
Układy wektorów współbieżnych są rozwiązywane za pomocą metod matematycznych lub wykresów, które są metodą równoległoboku sił i metody wieloboku sił. Dzięki temu zostanie określona wartość powstałego wektora, która wskazuje kierunek, w którym ciało się poruszy.
Zasadniczo główną różnicą między wektorami współliniowymi a wektorami współbieżnymi jest linia działania, w której działają: te współliniowe działają w tej samej linii, podczas gdy współbieżne w innej.
Oznacza to, że wektory współliniowe działają w jednej płaszczyźnie „X” lub „Y”; a jednoczesne działanie w obu płaszczyznach, począwszy od tego samego punktu.
Wektory współliniowe nie znajdują się w punkcie, podobnie jak współbieżne, ponieważ są do siebie równoległe.
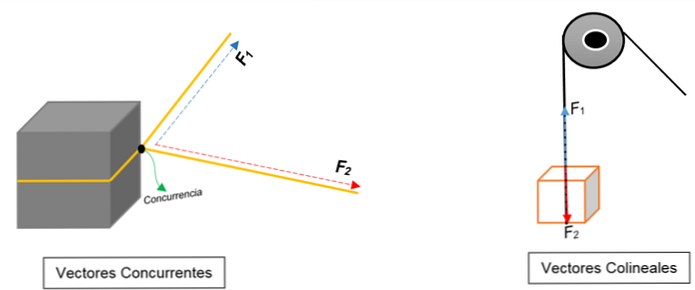
Na lewym obrazku widać blok. Jest związany liną, a węzeł dzieli go na dwie części; przy ciągnięciu w kierunku różnych orientacji iz różnymi siłami, blok przesunie się w tym samym kierunku.
Dwa wektory są reprezentowane w jednym punkcie (bloku), niezależnie od ich modułu, sensu lub kierunku.
Zamiast tego na prawym obrazku pojawia się koło pasowe, które podnosi pudełko. Lina reprezentuje linię działania; gdy zostanie pociągnięty, działają na niego dwie siły (wektory): jedna siła naprężenia (przy wspinaniu się na blok) i inna siła, która wywiera ciężar bloku. Oba mają ten sam kierunek, ale w przeciwnych kierunkach; nie zgadzaj się w jednym punkcie.
Referencje
- Estalella, J. J. (1988). Analiza wektorowa. Tom 1.
- Gupta, A. (s.f.). Tata McGraw-Hill Education.
- Jin Ho Kwak, S. H. (2015). Algebra liniowa. Springer Science & Business Media.
- Montiel, H. P. (2000). Fizyka 1 dla matury technicznej. Grupa redakcyjna Patria.
- Santiago Burbano de Ercilla, C. G. (2003). Fizyka ogólna Redakcja Tebar.
- Sinha, K. (s.f.). Książka tekstowa matematyki XII tom 2. Publikacje Rastogi.


