Ile osi symetrii ma koło?

The osie symetrii okręgu Są nieskończone. Te osie to te, które dzielą dowolny kształt geometryczny na dwie dokładnie równe połowy.

A okrąg składa się ze wszystkich punktów, których odległość do stałego punktu jest mniejsza lub równa pewnej wartości „r”.

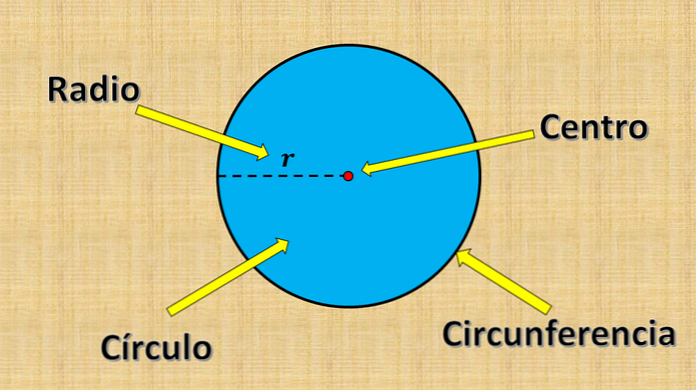
Wspomniany wyżej punkt stały nazywa się środkiem, a wartość „r” nazywa się promieniem. Promień jest największą odległością pomiędzy punktem na okręgu a środkiem.

Z drugiej strony, każdy segment linii, którego końce znajdują się na krawędzi okręgu (obwód) i przechodzący przez środek, nazywa się średnicą. Jego pomiar jest zawsze równy dwukrotności promienia.

Okrąg i obwód

Nie mylić okręgu z okręgiem. Obwód odnosi się tylko do punktów znajdujących się w odległości „r” od środka; to znaczy tylko krawędź okręgu.

Jednak patrząc na osie symetrii, obojętne jest, czy pracujesz z okręgiem, czy z okręgiem.

Jaka jest oś symetrii?

Oś symetrii to linia, która dzieli na dwie równe części pewną figurę geometryczną. Innymi słowy, oś symetrii działa jak lustro.

Wały symetrii koła

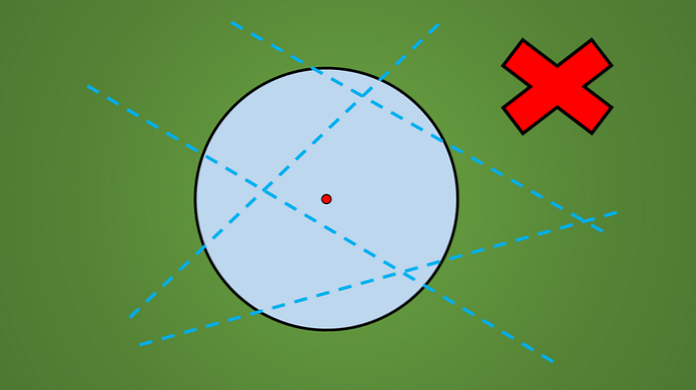
Jeśli zaobserwujesz dowolny okrąg, niezależnie od jego promienia, możesz zobaczyć, że nie każda linia, która go przecina, jest osią symetrii.

Na przykład żadna z linii narysowanych na poniższym obrazie nie jest osią symetrii.

Łatwym sposobem sprawdzenia, czy linia jest osią symetrii, czy nie, jest odbijanie prostopadle figury geometrycznej po przeciwnej stronie linii.

Jeśli odbicie nie pasuje do oryginalnej figury, to ta linia nie jest osią symetrii. Poniższy obraz ilustruje tę technikę.

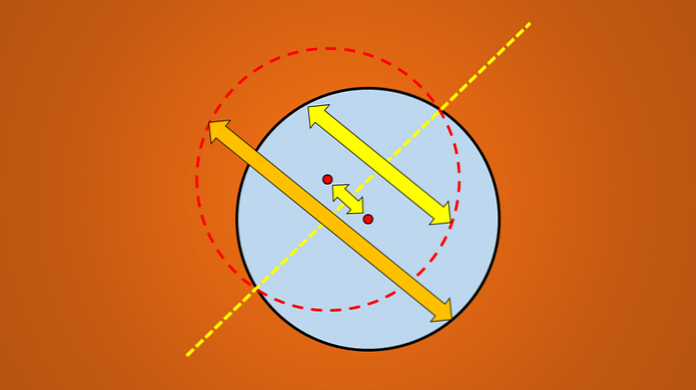
Ale jeśli uwzględni się poniższy obraz, dobrze wiadomo, że narysowana linia jest osią symetrii okręgu.

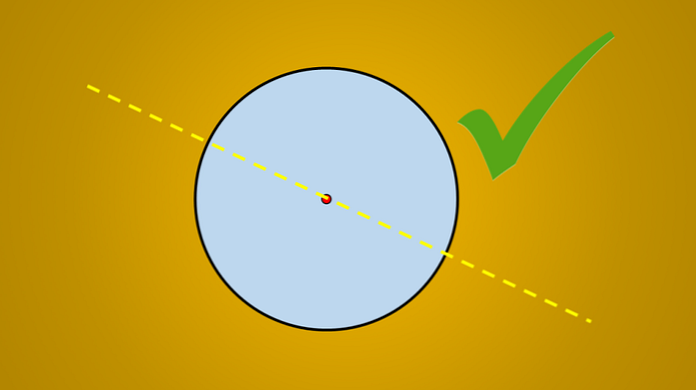
Pytanie brzmi: czy jest więcej osi symetrii? Odpowiedź brzmi: tak. Jeśli obrócisz tę linię o 45 ° w kierunku przeciwnym do ruchu wskazówek zegara, otrzymana linia jest również osią symetrii okręgu.

To samo dzieje się, jeśli obrócisz o 90 °, 30 °, 8 ° i ogólnie o dowolną liczbę stopni.

Ważną rzeczą w tych liniach nie jest ich nachylenie, ale wszystkie przechodzą przez środek okręgu. Dlatego każda linia zawierająca średnicę okręgu jest osią symetrii.

Ponieważ okrąg ma nieskończoną liczbę średnic, ma nieskończoną liczbę osi symetrii.

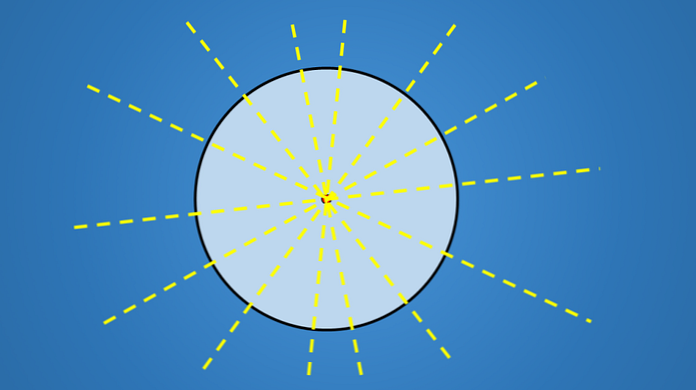
Inne figury geometryczne, takie jak trójkąt, czworokąt, pięciokąt, sześciokąt lub jakikolwiek inny wielokąt, mają skończoną liczbę osi symetrii.

Powodem, dla którego okrąg ma nieskończoną liczbę osi symetrii, jest to, że nie ma boków.

Referencje

1. Basto, J. R. (2014). Matematyka 3: Podstawowa geometria analityczna. Grupa redakcyjna Patria.
2. Billstein, R., Libeskind, S., i Lott, J. W. (2013). Matematyka: podejście do rozwiązywania problemów dla nauczycieli edukacji podstawowej. López Mateos Editores.
3. Bult, B., & Hobbs, D. (2001). Leksykon matematyczny (zilustrowane ed.). (F. P. Cadena, Trad.) Edycje AKAL.
4. Callejo, I., Aguilera, M., Martinez, L. i Aldea, C. (1986). Matematyka Geometria Zreformuj górny cykl E.G.B. Ministerstwo Edukacji.
5. Schneider, W. i Sappert, D. (1990). Praktyczny podręcznik rysunku technicznego: wprowadzenie do podstaw technicznego rysunku technicznego. Reverte.
6. Thomas, G. B. i Weir, M. D. (2006). Obliczanie: kilka zmiennych. Pearson Education.